Green Coordinates (patent pending)

Yaron Lipman David Levin Daniel Cohen-Or

ACM SIGGRAPH 2008

Abstract:

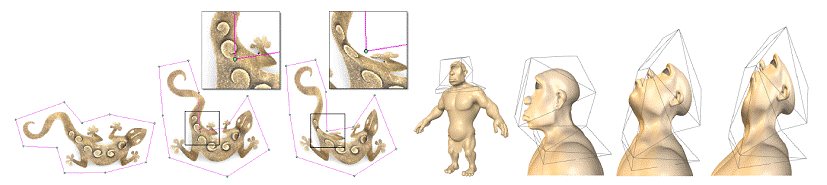
We introduce Green Coordinates for closed polyhedral cages. The

coordinates are motivated by Green’s third integral identity and respect

both the vertices position and faces orientation of the cage.

We show that Green Coordinates lead to space deformations with a

shape-preserving property. In particular, in 2D they induce conformal

mappings, and extend naturally to quasi-conformal mappings

in 3D. In both cases we derive closed-form expressions for the coordinates,

yielding a simple and fast algorithm for cage-based space

deformation. We compare the performance of Green Coordinates

with those of Mean Value Coordinates and Harmonic Coordinates

and show that the advantage of the shape-preserving property is not

achieved at the expense of speed or simplicity. We also show that

the new coordinates extend the mapping in a natural analytic manner

to the exterior of the cage, allowing the employment of partial

cages.

Technical Report:

Acrobat, ~7 MB