|
Parameterization-Free Projection For Geometry Reconstruction |
||||
|
|
||||
|
|
||||
|
ACM Transactions on Graphics (SIGGRAPH 2007) |
||||
|
Example videos of the projection operator: |
||||
|
|
||||
|
Abstract: |
||||
|
|
||||
|
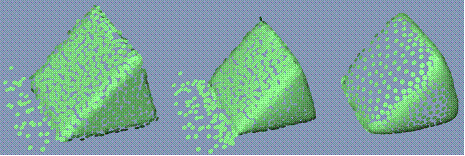
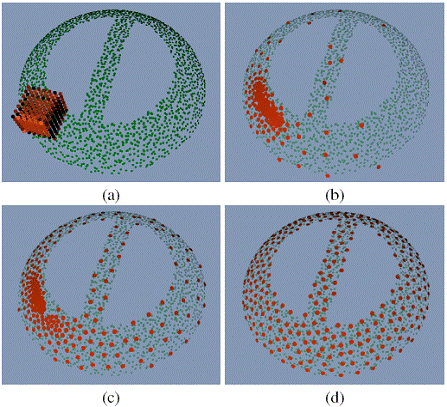
We introduce a Locally Optimal Projection operator (LOP) for surface approximation from point-set data. The operator is parameterization free, in the sense that it does not rely on estimating a local normal, fitting a local plane, or using any other local parametric representation. Therefore, it can deal with noisy data which clutters the orientation of the points. The method performs well in cases of ambiguous orientation, e.g., if two folds of a surface lie near each other, and other cases of complex geometry in which methods based upon local plane fitting may fail. Although defined by a global minimization problem, the method is effectively local, and it provides a second order approximation to smooth surfaces. Hence allowing good surface approximation without using any explicit or implicit approximation space. Furthermore, we show that LOP is highly robust to noise and outliers and demonstrate its effectiveness by applying it to raw scanned data of complex shapes. |
||||
|
|
||||
|
Technical Report: |
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
Examples: |
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
||||
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|
||||
|
|