


Next: Calculating the Derivative of
Up: No Title
Previous: Choosing the parameters for
TD-Gammon
Let
V*(s,0) be the probability of white
winning from state s and it is white's turn (assuming white and
black are playing optimally). Let
V*(s,1) be the probability
of white winning from state s and it is black's turn.
We estimate
V*(s,l) using a neural network which calculates
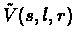 .
.
The Neural Network:
- 198 inputs.
- 40 nodes in the second level.
- 1 output node in the third level.
Network Initialization: (small) random weights.
Training Method: The program plays for both sides. For each
point in time we have a state st, a vector rt, and a
turn lt.
For each state s' accessible from st (according to the
dice), we calculate
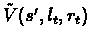 ,
and
choose the best state. (For white's turn choose the state
corresponding to the maximum value; for black's - the minimum.)
,
and
choose the best state. (For white's turn choose the state
corresponding to the maximum value; for black's - the minimum.)
Updating Parameters: At the end of each turn, we compute:
which is the TD (temporal difference). (In the final state we
replace
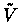 with the game outcome.) In addition,
we update
with the game outcome.) In addition,
we update
 :
:
At the end of each game a new game is started, and r0 is set
to the previous game's parameter vector.
- 1.
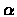 is set to a constant (determined by experiments).
is set to a constant (determined by experiments).
- 2.
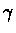 does not affect the results significantly in this case.
does not affect the results significantly in this case.
At the end of the training phase, we get a function
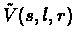 (r is fixed) which we can use to
play backgammon.
(r is fixed) which we can use to
play backgammon.
Improvements:
- Instead if 40 nodes at the second level, we add 40 more (80
total), the additional 40 units are set to represent important
patterns for backgammon.
- After
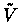 is set, it can be used
immediately (one step), or, alternatively, we can look a few steps
ahead, by building a game search tree.
is set, it can be used
immediately (one step), or, alternatively, we can look a few steps
ahead, by building a game search tree.
Comments:
-
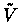 wasn't a good estimate for the
probability of white winning, but the policy derived from it is a
very good one. (the reason for this is as yet unclear.)
wasn't a good estimate for the
probability of white winning, but the policy derived from it is a
very good one. (the reason for this is as yet unclear.)
- The chosen policy is totally greedy (selected
deterministically). However, in backgammon there is a lot of
randomness, because of the dice. This enables us to "explore",
although we do not perform this explicitly.
- TD-Gammon has achieved a skill level close to the level of
the best players in the world today!



Next: Calculating the Derivative of
Up: No Title
Previous: Choosing the parameters for
Yishay Mansour
2000-01-17