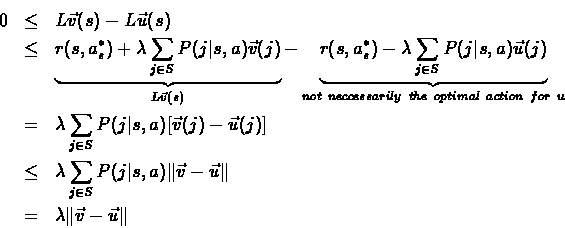Next: Example:
Up: The Solution of the
Previous: is a fixed point
Uniqueness of 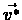
If
then
Hence
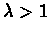 in contradiction to the premises.
in contradiction to the premises.
Thus 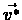 is unique.
is unique.

Next we will show that the operator L is a contracting
operator.
Claim 5.7
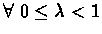
,
L is a contracting operator.
Proof:For all 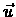 ,
,
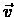 ,
we choose
,
we choose 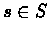 ,
and assume
,
and assume
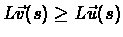 .
.
We define as* such that:
We have shown that
(The same proof holds for
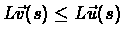 )
)
Thus, for all 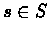 ,
,
Hence L is a contracting operator.

Proof:
- 1.
- As L has been shown to be a contracting operator there is a
unique solution for the equation Lv = v by theorem
![[*]](/usr/local/lib/latex2html-98.1p1/icons.gif/cross_ref_motif.gif) . This fixed point is
. This fixed point is
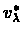 .
.
- 2.
- Is true by the same argument.




Next: Example:
Up: The Solution of the
Previous: is a fixed point
Yishay Mansour
1999-11-24
![]() ,
,
![]() ,
we choose
,
we choose ![]() ,
and assume
,
and assume
![]() .
.