


Next: Equality of schemes using
Up: Forward Updates Versus Backward
Previous: Forward Updates Versus Backward
Algorithm
The algorithm is as follows:
- 1.
- Define an arbitrary
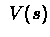 ,
,
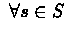 set
set
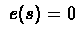
- 2.
- Repeat for every run : Set initial state
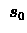
- 3.
- Repeat for every step of the run:
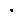 Choose action according to policy
Choose action according to policy
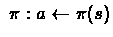
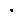 Perform action
Perform action 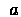 , receive next state
, receive next state 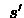 and immediate reward
and immediate reward 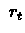
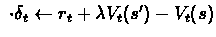
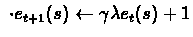
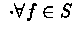 set
set
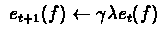 for
for
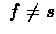 and
and
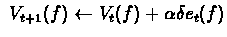
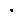 repeat steps 2,3 until final state is reached (for
every run)
repeat steps 2,3 until final state is reached (for
every run)
Using this scheme, we update previous values according to new
immediate reward and according to state we have reached. For more
distant states weight of the update is smaller and for more close
states the weight is larger.
Let us examine different values of 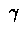 .
.
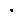 For
For
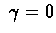 :
:
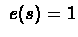 iff
iff
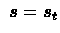 and
and
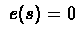 otherwise
otherwise
So, we will update only
current state according to received reward and we once again have
the TD(0) scheme.
 For
For
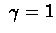 : e(s) is contribution of this
step to state s, i.e. if s is visited in the run in steps
: e(s) is contribution of this
step to state s, i.e. if s is visited in the run in steps
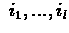 then
then
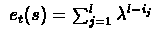
where
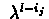 is
contribution of current step to step
is
contribution of current step to step 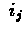
Although TD(1) resembles MC , there is a minor difference : MC
waits for the end of the run to perform updates while TD(1)
performs updates online. By the end of the run, both methods give
the same value function , but functions computed by TD(1) will be
hopefully more accurate during the run, since they are updated
online.



Next: Equality of schemes using
Up: Forward Updates Versus Backward
Previous: Forward Updates Versus Backward
Yishay Mansour
2000-01-06