Approximate Computation of Multidimensional Aggregates of
Sparse Data Using Wavelets
by
Jeffrey Scott Vitter
Min Wang
Summarized by Eyal
Baruch
Introduction
Counting multidimensional aggregates
in high dimensions is a performance bottleneck for many OLAP applications.
Obtaining the exact answer to an aggregation query can be prohibitively
expensive in terms of time and/or storage space in data warehouse environment.
It is advantageous to have fast, approximate answers to OLAP aggregation
queries.
This paper presents a new time efficient and storage
efficient algorithm which provides approximate answers to high dimensional
OLAP aggregation queries in massive sparse data.
Answering a Query
The new approach was developed for
the important case of sparse high-dimensional arrays, which often arise
in practice. It offers I/O efficiency, quick response time in answering
an on-line query, accuracy in answering a typical OLAP query and progressive
refinement of the approximate answers in case more accuracy is desired.
The new technique is based upon a multiresoultion
wavelet decomposition that yields an approximate representation of the
underlying multidimensional data. This space efficient representation
is called, compact data cube. The paper's authors used wavelet decomposition
procedure based on Haar basis, which are fast to compute and easy to implement.
The algorithm for constructing the data cube consists
of several passes. In each pass one group of the crude data (the partition
to groups is based upon internal memory space and disk block size) is processed
(i.e., an ordinary multidimensional wavelet decomposition is performed)
and the results are written out to be used for the next pass. By proper
buffer management, it can be ensured that the individual blocks on disk
never have to be read more than once while processing each group.
One problem is that the density of the intermediate results
will increase from pass to pass, since performing wavelet decomposition
on sparse data usually results in more nonzero coefficients. This may cause
to processing more and more entries from pass to pass, even though a lot
of entries are very small in magnitude. The natural solution to is truncation
(it is reasonable because it is in line with the wavelet decomposition
method itself, that is, the most significant wavelet coefficients contribute
the most to the reconstruction of the original signal). However, it is
too expensive to do truncation after all intermediate entries are written
out in a multipass process. Instead truncation is done in each pass via
an on-line statistical learning process.
After the original data is preprocessed, the result should
be much smaller so it fits in one or a small number of disk blocks, depending
upon the desired accuracy for the queries. Thus, given the storage limitations
for the compact data cube, it is possible to keep only a certain number
of wavelet coefficients. The process of determining which are the best
coefficients to keep, so as to minimize the error of approximation is called
thresholding. The paper suggests several ways to measure the error of approximation
for individual queries. Once it is done, a norm to measure the error of
a collection of queries should be obtained. The chosen ranking process
applied in the paper is a combination of the 2-norm and weight function,
which is proven to estimate the contribution of each coefficient to a range-sum
query (class of aggregation queries which are defined by summing up contiguous
domain range of some of the attributes).
In the on-line phase, for any given
query, the compact data cube is consulted to give an approximate answer
in one I/O or a small number of I/Os.
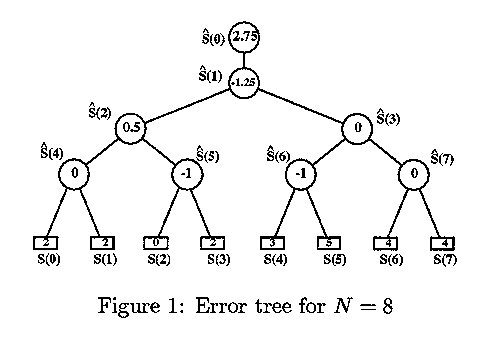
To fully understand the on-line query processing algorithm,
the relationship between wavelet coefficients and a range-sum query are
examined using the error tree structure. The error tree is built
based upon the wavelet transform procedure. It is a bottom-up process,
where each internal node is associated with a wavelet coefficient value,
and each leaf is associated with an original signal value. The construction
of the error tree exactly mirrors the wavelet transform procedure. It is
proven that the reconstruction of any signal value depends only upon the
values of those internal nodes along the path from the corresponding leaf
to the root. This leads to the construction (and also complexity evaluation)
of the on-line query algorithm, according to the first coefficients which
contribute to the range sum query.
Results and Conclusions
Experiments show that the compact data
cube provides excellent approximation for on-line range-sum queries with
limited space usage and little computational cost. The paper describes
the full algorithm in a very clear and consistent way. Most of the theorem
are proven using lemmas or are justified using the former paper of the
same authors. The improvements achieved are well explained and evaluated
in terms of complexity, sometimes even compared to results of other known
models.
Future Work
Future development of this approach
is possible in many directions. One way, is the use of special transform
for further improvements in relative accuracy (it is possible that such
transform are effective mainly in lower dimensions). Other possible improvements
can be obtained by quantizing the wavelet coefficients and entropy encoding
of the quantized coefficients. Even, new dynamic efficient algorithms are
being evolved for maintaining the compact data cube, when the underlying
raw data is changed.
