About me
I am an assistant professor at TAU working in the field of probability.
Publications (show abstracts)
Selected papers
-
Rigidity of proper colorings of $\mathbb{Z}^d$
Inventiones
A proper $q$-coloring of a domain in $\mathbb{Z}^d$ is a function assigning one of $q$ colors to each vertex of the domain such that adjacent vertices are colored differently. Sampling a proper $q$-coloring uniformly at random, does the coloring typically exhibit long-range order? It has been known since the work of Dobrushin that no such ordering can arise when $q$ is large compared with $d$. We prove here that long-range order does arise for each $q$ when $d$ is sufficiently high, and further characterize all periodic maximal-entropy Gibbs states for the model. Ordering is also shown to emerge in low dimensions if the lattice $\mathbb{Z}^d$ is replaced by $\mathbb{Z}^{d_1}\times\mathbb{T}^{d_2}$ with $d_1\ge 2$, $d=d_1+d_2$ sufficiently high and $\mathbb{T}$ a cycle of even length. The results address questions going back to Berker--Kadanoff (1980), Kotecký (1985) and Salas--Sokal (1997).
-
Long-range order in discrete spin systems
Preprint
We establish long-range order for discrete nearest-neighbor spin systems on $\mathbb{Z}^d$ satisfying a certain symmetry assumption, when the dimension $d$ is higher than an explicitly described threshold. The results characterize all periodic, maximal-pressure Gibbs states of the system. The results further apply in low dimensions provided that the lattice $\mathbb{Z}^d$ is replaced by $\mathbb{Z}^{d_1}\times\mathbb{T}^{d_2}$ with $d_1\ge 2$ and $d=d_1+d_2$ sufficiently high, where $\mathbb{T}$ is a cycle of even length. Applications to specific systems are discussed in detail and models for which new results are provided include the antiferromagnetic Potts model, Lipschitz height functions, and the hard-core, Widom--Rowlinson and beach models and their multi-type extensions.[arXiv]
-
Macroscopic loops in the loop O(n) model at Nienhuis' critical point
JEMS
(Journal of the European Mathematical Society)
The loop $O(n)$ model is a model for a random collection of non-intersecting loops on the hexagonal lattice, which is believed to be in the same universality class as the spin $O(n)$ model. It has been predicted by Nienhuis that for $0\le n\le 2$ the loop $O(n)$ model exhibits a phase transition at a critical parameter $x_c(n)=\tfrac{1}{\sqrt{2+\sqrt{2-n}}}$. For $0 \lt n\le 2$, the transition line has been further conjectured to separate a regime with short loops when $x\lt x_c(n)$ from a regime with macroscopic loops when $x\ge x_c(n)$.
In this paper, we prove that for $n\in [1,2]$ and $x=x_c(n)$ the loop $O(n)$ model exhibits macroscopic loops. This is the first instance in which a loop $O(n)$ model with $n\neq 1$ is shown to exhibit such behaviour. A main tool in the proof is a new positive association (FKG) property shown to hold when $n \ge 1$ and $0\lt x\le\frac{1}{\sqrt{n}}$. This property implies, using techniques recently developed for the random-cluster model, the following dichotomy: either long loops are exponentially unlikely or the origin is surrounded by loops at any scale (box-crossing property). We develop a 'domain gluing' technique which allows us to employ Smirnov's parafermionic observable to rule out the first alternative when $x=x_c(n)$ and $n\in[1,2]$. -
Finitary codings for spatial mixing Markov random fields
AOP
(Annals of Probability)
It has been shown by van den Berg and Steif that the sub-critical and critical Ising model on $\mathbb{Z}^d$ is a finitary factor of an i.i.d. process (ffiid), whereas the super-critical model is not. In fact, they showed that the latter is a general phenomenon in that a phase transition presents an obstruction for being ffiid. The question remained whether this is the only such obstruction. We make progress on this, showing that certain spatial mixing conditions (notions of weak dependence on boundary conditions, not to be confused with other notions of mixing in ergodic theory) imply ffiid. Our main result is that weak spatial mixing implies ffiid with power-law tails for the coding radius, and that strong spatial mixing implies ffiid with exponential tails for the coding radius. The weak spatial mixing condition can be relaxed to a condition which is satisfied by some critical two-dimensional models. Using a result of the author, we deduce that strong spatial mixing also implies ffiid with stretched-exponential tails from a finite-valued i.i.d. process.
We give several applications to models such as the Potts model, proper colorings, the hard-core model, the Widom--Rowlinson model and the beach model. For instance, for the ferromagnetic $q$-state Potts model on $\mathbb{Z}^d$ at inverse temperature $\beta$, we show that it is ffiid with exponential tails if $\beta$ is sufficiently small, it is ffiid if $\beta < \beta_c(q,d)$, it is not ffiid if $\beta > \beta_c(q,d)$ and, when $d=2$ and $\beta=\beta_c(q,d)$, it is ffiid if and only if $q \le 4$. -
A short proof of the discontinuity of phase transition in the planar random-cluster model with $q>4$
CMP
(Communications in Mathematical Physics)
The goal of this paper is to provide a short proof of the discontinuity of phase transition for the random-cluster model on the square lattice with parameter $q>4$. This result was recently shown via the so-called Bethe ansatz for the six-vertex model. Our proof also exploits the connection to the six-vertex model, but does not rely on the Bethe ansatz. Our argument is soft and only uses very basic properties of the random-cluster model (for example, we do not need the Russo--Seymour--Welsh theory).
-
Characterizations of amenability through stochastic domination and
finitary codings
Preprint
We establish new characterizations of amenability of graphs through two probabilistic notions: stochastic domination and finitary codings (also called finitary factors).
On the stochastic domination side, we show that the plus state of the Ising model at very low temperature stochastically dominates a high density Bernoulli percolation if and only if the underlying graph is nonamenable. This answers a question of Liggett and Steif. We prove a similar result for theinfinite cluster process
of Bernoulli percolation, which is of particular interest as this process is not monotone and does not possess any nice form of the domain Markov property. We also prove that the plus states of the Ising model at very low temperatures are stochastically ordered if and only if the graph is nonamenable. This answers a second question of Liggett and Steif. We further show that these stochastic domination results can be witnessed by invariant monotone couplings.
On the finitary coding side, we show that the plus state of the Ising model at very low temperature is a finitary factor of an i.i.d. process if and only if the underlying graph is nonamenable (assuming it supports a phase transition). We show a similar result for the infinite cluster process of a high-density Bernoulli percolation.
A main technique is to consider diluted processes, for which Holley's condition can be established. In order to compare two Ising models, we apply a dilution mechanism using lattice gas theory. Along the way we develop general tools to establish invariant domination when Holley's condition is satisfied. The finitary factor results are based on the stochastic domination results and a dynamical construction involving bounding chains, along with a new technique to analyze coupling from the past in infinite-range processes via a novel disease spreading model, which may be of independent interest.[arXiv]
Full list of papers
-
Optimal matchings of randomly perturbed lattices
Preprint
Consider a point process in Euclidean space obtained by perturbing the integer lattice with independent and identically distributed random vectors. Under mild assumptions on the law of the perturbations, we construct a translation-invariant perfect matching between this point process and the lattice, such that the matching distance has the same tail behavior as the hole probability of the point process, which is a natural lower bound.[arXiv]
-
Finitary codings and stochastic domination for Poisson representable processes
Preprint
Construct a random set by independently selecting each finite subset of the integers with some probability depending on the set up to translations and taking the union of the selected sets. We show that when the only sets selected with positive probability are pairs, such a random set is a finitary factor of an IID process, answering a question of Forsström, Gantert and Steif. More generally, we show that this is the case whenever the distribution induced by the size of the selected sets has sufficient exponential moments, and that the existence of some exponential moment is necessary. We further show that such a random set is stochastically dominated by a non-trivial Bernoulli percolation if and only if there is a finite exponential moment, thereby partially answering another question of Forsström et al. We also give a partial answer to a third question regarding a form of phase transition. These results also hold on $\mathbb{Z}^d$ with $d \ge 2$. In the one-dimensional case, under the condition that the distribution induced by the diameter of the selected sets has an exponential moment, we further show that such a random set is finitarily isomorphic to an IID process.[arXiv]
-
A new proof of finitary isomorphism for Markov chains
Preprint
We give a new proof of a result of Rudolph stating that a countable-state mixing Markov chain with exponential return times is finitarily isomorphic to an IID process. Besides being short and direct, our proof has the added benefit of working for processes of finite or infinite entropy.[arXiv]
-
On the local convergence of integer-valued Lipschitz functions on regular trees
Preprint
We study random integer-valued Lipschitz functions on regular trees. It was shown by Peled, Samotij and Yehudayoff that such functions are localized, however, finer questions about the structure of Gibbs measures remain unanswered. Our main result is that the weak limit of a uniformly chosen 1-Lipschitz function with 0 boundary condition on a $d$-ary tree of height $n$ exists as $n \to \infty$ if $2 \le d \le 7$, but not if $d \ge 8$, thereby partially answering a question of Peled, Samotij and Yehudayoff. For large $d$, the value at the root alternates between being almost entirely concentrated on 0 for even $n$ and being roughly uniform on $\{-1,0,1\}$ for odd $n$, leading to different limits as $n$ approaches infinity along evens or odds. For $d \ge 8$, the essence of this phenomenon is preserved, which obstructs the convergence. For $d \le 7$, this phenomenon ceases to exist, and the law of the value at the root loses its connection with the parity of $n$. Along the way, we also obtain an alternative proof of localization. The key idea is a fixed point convergence result for a related operator on $\ell^\infty$, and a procedure to show that the iterations get into a
basin of attraction
of the fixed point.
We also prove some accompanying analogouseven-odd phenomenon
type results about $M$-lipschitz functions on general non-amenable graphs with high enough expansion (this includes for example the large $d$ case for regular trees). We also prove a convergence result for 1-Lipschitz functions with $\{0,1\}$ boundary condition. This last result relies on an absolute value FKG for uniform 1-Lipschitz functions when shifted by $1/2$.[arXiv] -
Characterizations of amenability through stochastic domination and
finitary codings
Preprint
We establish new characterizations of amenability of graphs through two probabilistic notions: stochastic domination and finitary codings (also called finitary factors).
On the stochastic domination side, we show that the plus state of the Ising model at very low temperature stochastically dominates a high density Bernoulli percolation if and only if the underlying graph is nonamenable. This answers a question of Liggett and Steif. We prove a similar result for theinfinite cluster process
of Bernoulli percolation, which is of particular interest as this process is not monotone and does not possess any nice form of the domain Markov property. We also prove that the plus states of the Ising model at very low temperatures are stochastically ordered if and only if the graph is nonamenable. This answers a second question of Liggett and Steif. We further show that these stochastic domination results can be witnessed by invariant monotone couplings.
On the finitary coding side, we show that the plus state of the Ising model at very low temperature is a finitary factor of an i.i.d. process if and only if the underlying graph is nonamenable (assuming it supports a phase transition). We show a similar result for the infinite cluster process of a high-density Bernoulli percolation.
A main technique is to consider diluted processes, for which Holley's condition can be established. In order to compare two Ising models, we apply a dilution mechanism using lattice gas theory. Along the way we develop general tools to establish invariant domination when Holley's condition is satisfied. The finitary factor results are based on the stochastic domination results and a dynamical construction involving bounding chains, along with a new technique to analyze coupling from the past in infinite-range processes via a novel disease spreading model, which may be of independent interest.[arXiv] - Random walks on regular trees can not be slowed down EJP (Electronic Journal of Probability) with Omer Angel, Jacob Richey and Amir Yehudayoff
-
Entropy-efficient finitary codings
JMD (Journal of Modern Dynamics)
We show that any finite-entropy, countable-valued finitary factor of an i.i.d. process can also be expressed as a finitary factor of a finite-valued i.i.d. process whose entropy is arbitrarily close to the target process. As an application, we give an affirmative answer to a question of van den Berg and Steif about the critical Ising model on $\mathbb{Z}^d$. En route, we prove several results about finitary isomorphisms and finitary factors. Our results are developed in a new framework for processes invariant to a permutation group of a countable set satisfying specific properties. This new framework includes all "classical" processes over countable amenable groups and all invariant processes on transitive amenable graphs with "uniquely centered balls". Some of our results are new already for $\mathbb{Z}$-processes. We prove a relative version of Smorodinsky's isomorphism theorem for finitely dependent $\mathbb{Z}$-processes. We also extend the Keane--Smorodinsky finitary isomorphism theorem to countable-valued i.i.d. processes and to i.i.d. processes taking values in a Polish space.
-
Independent sets in random subgraphs of the hypercube
Preprint
Let $Q_{d,p}$ be the random subgraph of the $d$-dimensional hypercube $\{0,1\}^d$, where each edge is retained independently with probability $p$. We study the asymptotic number of independent sets in $Q_{d,p}$ as $d \to \infty$ for a wide range of parameters $p$, including values of $p$ tending to zero as fast as $\frac{C\log d}{d^{1/3}}$, constant values of $p$, and values of $p$ tending to one. The results extend to the hardcore model on $Q_{d,p}$, and are obtained by studying the closely related antiferromagnetic Ising model on the hypercube, which can be viewed as a positive-temperature hardcore model on the hypercube. These results generalize previous results by Galvin, Jenssen and Perkins on the hard-core model on the hypercube, corresponding to the case $p=1$, which extended Korshunov and Sapozhenko's classical result on the asymptotic number of independent sets in the hypercube.[arXiv]
-
Uniform even subgraphs and graphical representations of Ising as factors of i.i.d.
EJP
(Electronic Journal of Probability)
We prove that the Loop $O(1)$ model, a well-known graphical expansion of the Ising model, is a factor of i.i.d. on unimodular random rooted graphs under various conditions, including in the presence of a non-negative external field. As an application we show that the gradient of the free Ising model is a factor of i.i.d. on unimodular planar maps having a locally finite dual. The key idea is to develop an appropriate theory of local limits of uniform even subgraphs with various boundary conditions and prove that they can be sampled as a factor of i.i.d. Another key tool we prove and exploit is that the wired uniform spanning tree on a unimodular transient graph is a factor of i.i.d. This partially answers some questions posed by Hutchcroft.
-
A tale of two balloons
PTRF
(Probability Theory and Related Fields)
From each point of a Poisson point process start growing a balloon at rate 1. When two balloons touch, they pop and disappear. Is every point contained in balloons infinitely often or not? We answer this for the Euclidean space, the hyperbolic plane and regular trees.
The result for the Euclidean space relies on a novel 0-1 law for stationary processes. Towards establishing the results for the hyperbolic plane and regular trees, we prove an upper bound on the density of any well-separated set in a regular tree which is a factor of an i.i.d. process. -
Long-range order in discrete spin systems
Preprint
We establish long-range order for discrete nearest-neighbor spin systems on $\mathbb{Z}^d$ satisfying a certain symmetry assumption, when the dimension $d$ is higher than an explicitly described threshold. The results characterize all periodic, maximal-pressure Gibbs states of the system. The results further apply in low dimensions provided that the lattice $\mathbb{Z}^d$ is replaced by $\mathbb{Z}^{d_1}\times\mathbb{T}^{d_2}$ with $d_1\ge 2$ and $d=d_1+d_2$ sufficiently high, where $\mathbb{T}$ is a cycle of even length. Applications to specific systems are discussed in detail and models for which new results are provided include the antiferromagnetic Potts model, Lipschitz height functions, and the hard-core, Widom--Rowlinson and beach models and their multi-type extensions.[arXiv]
-
Proper 3-colorings of $\mathbb{Z}^2$ are Bernoulli
ETDS
(Ergodic Theory and Dynamical Systems)
We consider the unique measure of maximal entropy for proper 3-colorings of $\mathbb{Z}^2$, or equivalently, the so-called zero-slope Gibbs measure. Our main result is that this measure is Bernoulli, or equivalently, that it can be expressed as the image of a translation-equivariant function of independent and identically distributed random variables placed on $\mathbb{Z}^2$. Along the way, we obtain various estimates on the mixing properties of this measure.
-
Three lectures on random proper colorings of $\mathbb{Z}^d$
Preprint
A proper $q$-coloring of a graph is an assignment of one of $q$ colors to each vertex of the graph so that adjacent vertices are colored differently. Sample uniformly among all proper $q$-colorings of a large discrete cube in the integer lattice $\mathbb{Z}^d$. Does the random coloring obtained exhibit any large-scale structure? Does it have fast decay of correlations? We discuss these questions and the way their answers depend on the dimension $d$ and the number of colors $q$. The questions are motivated by statistical physics (anti-ferromagnetic materials, square ice), combinatorics (proper colorings, independent sets) and the study of random Lipschitz functions on a lattice. The discussion introduces a diverse set of tools, useful for this purpose and for other problems, including spatial mixing, entropy and coupling methods, Gibbs measures and their classification and refined contour analysis.[arXiv]
-
Geometric random graphs on circles
CLAPEM
(Advances in Probability and Mathematical Statistics, Proceeding of CLAPEM 2019)
Given a dense countable set in a metric space, the infinite random geometric graph is the random graph with the given vertex set and where any two points at distance less than 1 are connected, independently, with some fixed probability. It has been observed by Bonato and Janssen that in some, but not all, such settings, the resulting graph does not depend on the random choices, in the sense that it is almost surely isomorphic to a fixed graph. While this notion makes sense in the general context of metric spaces, previous work has been restricted to sets in Banach spaces. We study the case when the underlying metric space is a circle of circumference $L$, and find a surprising dependency of behavior on the rationality of $L$.
-
Finitary isomorphisms of renewal point processes and continuous-time regenerative processes
IJM
(Israel Journal of Mathematics)
We show that a large class of stationary continuous-time regenerative processes are finitarily isomorphic to one another. The key is showing that any stationary renewal point process whose jump distribution is absolutely continuous with exponential tails is finitarily isomorphic to a Poisson point process. We further give simple necessary and sufficient conditions for a renewal point process to be finitarily isomorphic to a Poisson point process. This improves results and answers several questions of Soo and of Kosloff and Soo.
-
Finitary codings for gradient models and a new graphical representation for the six-vertex model
RSA
(Random Structures and Algorithms)
It is known that the Ising model on $\mathbb {Z}^d$ at a given temperature is a finitary factor of an i.i.d. process if and only if the temperature is at least the critical temperature. Below the critical temperature, the plus and minus states of the Ising model are distinct and differ from one another by a global flip of the spins. We show that it is only this global information which poses an obstruction for being finitary by showing that the gradient of the Ising model is a finitary factor of i.i.d. at all temperatures. As a consequence, we deduce a volume-order large deviation estimate for the energy. A similar result is shown for the Potts model.
A result in the same spirit is also shown for the six-vertex model, which is itself the gradient of a height function, with parameter $c \gtrapprox 6.4$. We show that the gradient of the height function is not a finitary factor of an i.i.d. process, but that its "Laplacian" is. For this, we introduce a coupling between the six-vertex model with $c\ge 2$ and a new graphical representation of it, reminiscent of the Edwards--Sokal coupling between the Potts and random-cluster models. We believe that this graphical representation may be of independent interest and could serve as a tool in further understanding of the six-vertex model.
To provide further support for the ubiquity of this type of phenomenon, we also prove an analogous result for the so-called beach model.
The tools and techniques used in this paper are probabilistic in nature. The heart of the argument is to devise a suitable tree structure on the clusters of the underlying percolation process (associated to the graphical representation of the given model), which can be revealed piece-by-piece via exploration. -
Markov chains with exponential return times are finitary
ETDS
(Ergodic Theory and Dynamical Systems)
Consider an ergodic Markov chain on a countable state space for which the return times have exponential tails. We show that the stationary version of any such chain is a finitary factor of an i.i.d. process. A key step is to show that any stationary renewal process whose jump distribution has exponential tails and is not supported on a proper subgroup of $\mathbb{Z}$ is a finitary factor of an i.i.d. process.
-
A short proof of the discontinuity of phase transition in the planar random-cluster model with $q>4$
CMP
(Communications in Mathematical Physics)
The goal of this paper is to provide a short proof of the discontinuity of phase transition for the random-cluster model on the square lattice with parameter $q>4$. This result was recently shown via the so-called Bethe ansatz for the six-vertex model. Our proof also exploits the connection to the six-vertex model, but does not rely on the Bethe ansatz. Our argument is soft and only uses very basic properties of the random-cluster model (for example, we do not need the Russo--Seymour--Welsh theory).
-
Mixing properties of colorings of the $\mathbb{Z}^d$ lattice
CPC
(Combinatorics, Probability and Computing)
We study and classify proper $q$-colorings of the $\mathbb Z^d$ lattice, identifying three regimes where different combinatorial behavior holds: (1) When $q\le d+1$, there exist frozen colorings, that is, proper $q$-colorings of $\mathbb Z^d$ which cannot be modified on any finite subset. (2) We prove a strong list-coloring property which implies that, when $q\ge d+2$, any proper $q$-coloring of the boundary of a box of side length $n \ge d+2$ can be extended to a proper $q$-coloring of the entire box. (3) When $q\geq 2d+1$, the latter holds for any $n \ge 1$. Consequently, we classify the space of proper $q$-colorings of the $\mathbb Z^d$ lattice by their mixing properties.
-
Pairwise optimal coupling of multiple random variables
Preprint
We generalize the optimal coupling theorem to multiple random variables: Given a collection of random variables, it is possible to couple all of them so that any two differ with probability comparable to the total-variation distance between them. In a number of cases we show that the disagreement probability we achieve is the best possible. The proofs of sharpness rely on new results in extremal combinatorics, which may be of independent interest.[arXiv]
-
Finitely dependent processes are finitary
AOP
(Annals of Probability)
We show that any finitely dependent invariant process on a transitive amenable graph is a finitary factor of an i.i.d. process. With an additional assumption on the geometry of the graph, namely that no two balls with different centers are identical, we further show that the i.i.d. process may be taken to have entropy arbitrarily close to that of the finitely dependent process. As an application, we give an affirmative answer to a question of Holroyd.
-
Rigidity of proper colorings of $\mathbb{Z}^d$
Inventiones
A proper $q$-coloring of a domain in $\mathbb{Z}^d$ is a function assigning one of $q$ colors to each vertex of the domain such that adjacent vertices are colored differently. Sampling a proper $q$-coloring uniformly at random, does the coloring typically exhibit long-range order? It has been known since the work of Dobrushin that no such ordering can arise when $q$ is large compared with $d$. We prove here that long-range order does arise for each $q$ when $d$ is sufficiently high, and further characterize all periodic maximal-entropy Gibbs states for the model. Ordering is also shown to emerge in low dimensions if the lattice $\mathbb{Z}^d$ is replaced by $\mathbb{Z}^{d_1}\times\mathbb{T}^{d_2}$ with $d_1\ge 2$, $d=d_1+d_2$ sufficiently high and $\mathbb{T}$ a cycle of even length. The results address questions going back to Berker--Kadanoff (1980), Kotecký (1985) and Salas--Sokal (1997).
-
Finitary codings for the random-cluster model and other infinite-range monotone models
EJP
(Electronic Journal of Probability)
A random field $X = (X_v)_{v \in G}$ on a quasi-transitive graph $G$ is a factor of i.i.d. if it can be written as $X=\varphi(Y)$ for some i.i.d. process $Y= (Y_v)_{v \in G}$ and equivariant map $\varphi$. Such a map, also called a coding, is finitary if, for every vertex $v \in G$, there exists a finite (but random) set $U \subset G$ such that $X_v$ is determined by $\{Y_u\}_{u \in U}$. We construct a coding for the random-cluster model on $G$, and show that the coding is finitary whenever the free and wired measures coincide. This strengthens a result of Häggström--Jonasson--Lyons. We also prove that the coding radius has exponential tails in the subcritical regime. As a corollary, we obtain a similar coding for the subcritical Potts model.
Our methods are probabilistic in nature, and at their heart lies the use of coupling-from-the-past for the Glauber dynamics. These methods apply to any monotone model satisfying mild technical (but natural) requirements. Beyond the random-cluster and Potts models, we describe two further applications -- the loop $O(n)$ model and long-range Ising models. In the case of $G = \mathbb{Z}^d$, we also construct finitary, translation-equivariant codings using a finite-valued i.i.d. process $Y$. To do this, we extend a mixing-time result of Martinelli--Olivieri to infinite-range monotone models on quasi-transitive graphs of sub-exponential growth. -
Finitary codings for spatial mixing Markov random fields
AOP
(Annals of Probability)
It has been shown by van den Berg and Steif that the sub-critical and critical Ising model on $\mathbb{Z}^d$ is a finitary factor of an i.i.d. process (ffiid), whereas the super-critical model is not. In fact, they showed that the latter is a general phenomenon in that a phase transition presents an obstruction for being ffiid. The question remained whether this is the only such obstruction. We make progress on this, showing that certain spatial mixing conditions (notions of weak dependence on boundary conditions, not to be confused with other notions of mixing in ergodic theory) imply ffiid. Our main result is that weak spatial mixing implies ffiid with power-law tails for the coding radius, and that strong spatial mixing implies ffiid with exponential tails for the coding radius. The weak spatial mixing condition can be relaxed to a condition which is satisfied by some critical two-dimensional models. Using a result of the author, we deduce that strong spatial mixing also implies ffiid with stretched-exponential tails from a finite-valued i.i.d. process.
We give several applications to models such as the Potts model, proper colorings, the hard-core model, the Widom--Rowlinson model and the beach model. For instance, for the ferromagnetic $q$-state Potts model on $\mathbb{Z}^d$ at inverse temperature $\beta$, we show that it is ffiid with exponential tails if $\beta$ is sufficiently small, it is ffiid if $\beta < \beta_c(q,d)$, it is not ffiid if $\beta > \beta_c(q,d)$ and, when $d=2$ and $\beta=\beta_c(q,d)$, it is ffiid if and only if $q \le 4$. -
Finitary coding for the sub-critical Ising model with finite expected coding volume
EJP
(Electronic Journal of Probability)
It has been shown by van den Berg and Steif that the sub-critical Ising model on $\mathbb{Z}^d$ is a finitary factor of a finite-valued i.i.d. process. We strengthen this by showing that the factor map can be made to have finite expected coding volume (in fact, stretched-exponential tails), answering a question of van den Berg and Steif. The result holds at any temperature above the critical temperature. An analogous result holds for Markov random fields satisfying a high-noise assumption and for proper colorings with a large number of colors.
-
A condition for long-range order in discrete spin systems with application to the antiferromagnetic Potts model
Preprint
We give a general condition for a discrete spin system with nearest-neighbor interactions on the $\mathbb{Z}^d$ lattice to exhibit long-range order. The condition is applicable to systems with residual entropy in which the long-range order is entropically driven. As a main example we consider the antiferromagnetic $q$-state Potts model and rigorously prove the existence of a broken sub-lattice symmetry phase at low temperature and high dimension -- a new result for $q\ge 4$. As further examples, we prove the existence of an ordered phase in a clock model with hard constraints and extend the known regime of the demixed phase in the lattice Widom-Rowlinson model.[arXiv]
-
Lectures on the spin and loop O(n) models
Sojourns in PT&SP
(Sojourns in Probability Theory and Statistical Physics)
The classical spin $O(n)$ model is a model on a $d$-dimensional lattice in which a vector on the $(n-1)$-dimensional sphere is assigned to every lattice site and the vectors at adjacent sites interact ferromagnetically via their inner product. Special cases include the Ising model ($n=1$), the XY model ($n=2$) and the Heisenberg model ($n=3$). We discuss questions of long-range order and decay of correlations in the spin $O(n)$ model for different combinations of the lattice dimension $d$ and the number of spin components $n$.
The loop $O(n)$ model is a model for a random configuration of disjoint loops. We discuss its properties on the hexagonal lattice. The model is parameterized by a loop weight $n\ge0$ and an edge weight $x\ge 0$. Special cases include self-avoiding walk ($n=0$), the Ising model ($n=1$), critical percolation ($n=x=1$), dimer model ($n=1,x=\infty$), proper $4$-coloring ($n=2, x=\infty)$, integer-valued ($n=2$) and tree-valued (integer $n>=3$) Lipschitz functions and the hard hexagon model ($n=\infty$). The object of study in the model is the typical structure of loops. We review the connection of the model with the spin $O(n)$ model and discuss its conjectured phase diagram, emphasizing the many open problems remaining. -
Macroscopic loops in the loop O(n) model at Nienhuis' critical point
JEMS
(Journal of the European Mathematical Society)
The loop $O(n)$ model is a model for a random collection of non-intersecting loops on the hexagonal lattice, which is believed to be in the same universality class as the spin $O(n)$ model. It has been predicted by Nienhuis that for $0\le n\le 2$ the loop $O(n)$ model exhibits a phase transition at a critical parameter $x_c(n)=\tfrac{1}{\sqrt{2+\sqrt{2-n}}}$. For $0 \lt n\le 2$, the transition line has been further conjectured to separate a regime with short loops when $x\lt x_c(n)$ from a regime with macroscopic loops when $x\ge x_c(n)$.
In this paper, we prove that for $n\in [1,2]$ and $x=x_c(n)$ the loop $O(n)$ model exhibits macroscopic loops. This is the first instance in which a loop $O(n)$ model with $n\neq 1$ is shown to exhibit such behaviour. A main tool in the proof is a new positive association (FKG) property shown to hold when $n \ge 1$ and $0\lt x\le\frac{1}{\sqrt{n}}$. This property implies, using techniques recently developed for the random-cluster model, the following dichotomy: either long loops are exponentially unlikely or the origin is surrounded by loops at any scale (box-crossing property). We develop a 'domain gluing' technique which allows us to employ Smirnov's parafermionic observable to rule out the first alternative when $x=x_c(n)$ and $n\in[1,2]$. -
The growth constant of odd cutsets in high dimensions
CPC
(Combinatorics, Probability and Computing)
A cutset is a non-empty finite subset of $\mathbb{Z}^d$ which is both connected and co-connected. A cutset is odd if its vertex boundary lies in the odd bipartition class of $\mathbb{Z}^d$. Peled suggested that the number of odd cutsets which contain the origin and have $n$ boundary edges may be of order $e^{\Theta(n/d)}$ as $d \to \infty$, much smaller than the number of general cutsets, which was shown by Lebowitz and Mazel to be of order $d^{\Theta(n/d)}$. In this paper, we verify this by showing that the number of such odd cutsets is $(2+o(1))^{n/2d}$.
-
Long-range order in the 3-state antiferromagnetic Potts model in high dimensions
JEMS
(Journal of the European Mathematical Society)
We prove the existence of long-range order for the 3-state Potts antiferromagnet at low temperature on $\mathbb{Z}^d$ for sufficiently large $d$. In particular, we show the existence of six extremal and ergodic infinite-volume Gibbs measures, which exhibit spontaneous magnetization in the sense that vertices in one bipartition class have a much higher probability to be in one state than in either of the other two states. This settles the high-dimensional case of the Kotecký conjecture.
-
On the converse of Talagrand's influence inequality
Preprint
In 1994, Talagrand showed a generalization of the celebrated KKL theorem. In this work, we prove that the converse of this generalization also holds. Namely, for any sequence of numbers $0\lt a_1,a_2,\ldots,a_n\le 1$ such that $\sum_{j=1}^n a_j/(1-\log a_j)\ge C$ for some constant $C>0$, it is possible to find a roughly balanced Boolean function $f$ such that $\textrm{Inf}_j[f] \lt a_j$ for every $1 \le j \le n$.[arXiv]
-
Exponential decay of loop lengths in the loop O(n) model with large n
CMP
(Communications in Mathematical Physics)
The loop $O(n)$ model is a model for a random collection of non-intersecting loops on the hexagonal lattice, which is believed to be in the same universality class as the spin $O(n)$ model. It has been conjectured that both the spin and the loop $O(n)$ models exhibit exponential decay of correlations when $n>2$. We verify this for the loop $O(n)$ model with large parameter $n$, showing that long loops are exponentially unlikely to occur, uniformly in the edge weight $x$. Our proof provides further detail on the structure of typical configurations in this regime. Putting appropriate boundary conditions, when $nx^6$ is sufficiently small, the model is in a dilute, disordered phase in which each vertex is unlikely to be surrounded by any loops, whereas when $nx^6$ is sufficiently large, the model is in a dense, ordered phase which is a small perturbation of one of the three ground states.
-
Random walk with long-range constraints
EJP
(Electronic Journal of Probability)
We consider a model of a random height function with long-range constraints on a discrete segment. This model was suggested by Benjamini, Yadin and Yehudayoff and is a generalization of simple random walk. The random function is uniformly sampled from all graph homomorphisms from the graph $P_{n,d}$ to the integers $\mathbb{Z}$, where the graph $P_{n,d}$ is the discrete segment $\{0,1,..., n\}$ with edges between vertices of different parity whose distance is at most $2d+1$. Such a graph homomorphism can be viewed as a height function whose values change by exactly one along edges of the graph $P_{n,d}$. We also consider a similarly defined model on the discrete torus.
Benjamini, Yadin and Yehudayoff conjectured that this model undergoes a phase transition from a delocalized to a localized phase when $d$ grows beyond a threshold $c*\log(n)$. We establish this conjecture with the precise threshold $\log_2(n)$. Our results provide information on the typical range and variance of the height function for every given pair of $n$ and $d$, including the critical case when $d-\log_2(n)$ tends to a constant.
In addition, we identify the local limit of the model, when $d$ is constant and $n$ tends to infinity, as an explicitly defined Markov chain.
Coauthors
Some Pictures
The spin O(n) model
The Ising model (n=1)
 beta=0.4
beta=0.4
 beta=0.4407 (critical)
beta=0.4407 (critical)
 beta=0.5
beta=0.5
 beta=0.5 with Dobrushin b.c.
beta=0.5 with Dobrushin b.c.
The XY model (n=2)
 beta=1
beta=1
 beta=1.12 (critical)
beta=1.12 (critical)
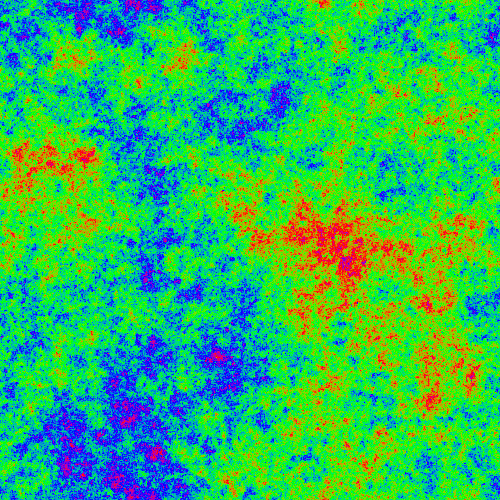 beta=1.5
beta=1.5
 beta=3
beta=3
The Heisenberg model (n=3)
 beta=2
beta=2
 beta=10
beta=10
3-colorings (the antiferromagnetic Potts model)
 2D, beta=4
2D, beta=4
 slab in 3D, beta=4
slab in 3D, beta=4