


Next: About this document ...
Up: Linear Programming
Previous: A Linear Programming Example
Use of
Linear Programming to Find the Optimal Policy
The general
translation of the problem
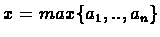 to a linear
program is as follows:
to a linear
program is as follows:
Minimize: x
Subject To:
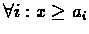
It was shown that the Optimality Equations of the discounted
infinite horizon problem are:
Using the above translation we would get the following linear
program:
Minimize:
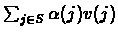
Subject To:
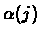 is any set of constants with the following
characteristics:
These constants can be viewed as the probability
distribution of the agent's initial state in the MDP.
is any set of constants with the following
characteristics:
These constants can be viewed as the probability
distribution of the agent's initial state in the MDP.
Accordingly, the dual linear program would be:
Maximize:
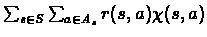
Subject To:
Intuitively, 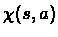 can be thought of as the
probability of being in state s and performing action a, while taking into account
the discount factor -
can be thought of as the
probability of being in state s and performing action a, while taking into account
the discount factor - 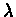 .
In the following theorem
.
In the following theorem
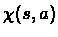 is defined more formally.
is defined more formally.
Theorem ![[*]](/usr/local/lib/latex2html-98.1p1/icons.gif/cross_ref_motif.gif) is assuring that every solution to the dual linear
program can be translated to a policy with a return value equal to
the maximized element in the program. Thus, the best solution of
the program can be translated to a policy with the maximal
possible return value. This policy will, obviously, be the best
policy.
is assuring that every solution to the dual linear
program can be translated to a policy with a return value equal to
the maximized element in the program. Thus, the best solution of
the program can be translated to a policy with the maximal
possible return value. This policy will, obviously, be the best
policy.



Next: About this document ...
Up: Linear Programming
Previous: A Linear Programming Example
Yishay Mansour
1999-12-18
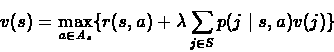
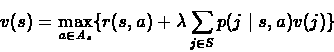
![\begin{eqnarray*}\chi_{d}(s,a) = \sum_{j\in S}\alpha(j)
\sum_{n=1}^{\infty}\lambda^{n-1} Prob[x_{n}=s\bigwedge y_{n}=a\mid
x_{1}=j]
\end{eqnarray*}](img129.gif)
![\begin{eqnarray*}Prob[d_{x}(s)=a]=\frac{\chi(s,a)}{\sum_{\overline{a} \in
A_{s}}\chi(s,\overline{a})}
\end{eqnarray*}](img131.gif)
![]() is assuring that every solution to the dual linear
program can be translated to a policy with a return value equal to
the maximized element in the program. Thus, the best solution of
the program can be translated to a policy with the maximal
possible return value. This policy will, obviously, be the best
policy.
is assuring that every solution to the dual linear
program can be translated to a policy with a return value equal to
the maximized element in the program. Thus, the best solution of
the program can be translated to a policy with the maximal
possible return value. This policy will, obviously, be the best
policy.